Hyperparameters of Dirty models

The aim of this example is to show how Dirty models change with the choice of their tuning hyperparameters.

DirtyModel estimates a set of sparse coefficients for multiple regression models that share a fraction of non-zero features. It is a generalization of The GroupLasso estimator. It also takes a 3D X (n_tasks, n_samples, n_features) and a 2D y (n_tasks, n_samples).

DirtyModel solves the optimization problem:

(1 / (2 * n_samples)) * ||Y - X(W_1 + W_2)||^2_Fro + alpha * ||W_1||_21
+ beta * ||W_2||_1

Where:

||W||_21 = \sum_i \sqrt{\sum_j w_ij^2}

i.e. the sum of norm of each row. and:

||W||_1 = \sum_i \sum_j |w_ij|

Some choices of alpha and beta eventually cancel out W_1 or W_2 entirely. The optimality condition of the optimization problem above leads to:

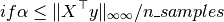
and:

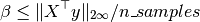
Then we have the sufficient conditions:

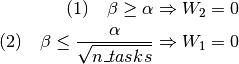
(1) leads to a Group Lasso estimator, (2) leads to an independent Lasso with the same beta for all tasks.

# Author: Hicham Janati (hicham.janati@inria.fr)
#
# License: BSD (3-clause)

import numpy as np

from mutar import DirtyModel

from matplotlib import pyplot as plt
from matplotlib.patches import Patch
from matplotlib.lines import Line2D

Generate multi-task data

rng = np.random.RandomState(42)
n_tasks, n_samples, n_features = 5, 20, 50
X = rng.randn(n_tasks, n_samples, n_features)

# generate random coefficients and make it sparse
# select support
support = rng.rand(n_features, n_tasks) > 0.95
coef = support * rng.randn(n_features, n_tasks)

# make features 0, 2, 4 and 6 shared
coef[:7:2] = rng.randn(4, n_tasks)

y = np.array([x.dot(c) for x, c in zip(X, coef.T)])

# add noise
y += 0.25 * np.std(y) + rng.randn(n_tasks, n_samples)

We create a grid of hyperparameters

xty = np.array([xx.T.dot(yy) for xx, yy in zip(X, y)])
beta_max = abs(xty).max() / n_samples
alpha_max = np.linalg.norm(xty, axis=0).max() / n_samples
alphas = np.linspace(0.02, 1.1, 40) * alpha_max
betas = np.linspace(0.02, 1.1, 40) * beta_max

alphas_mesh, betas_mesh = np.meshgrid(alphas, alphas)
alphas_mesh = alphas_mesh.flatten()
betas_mesh = betas_mesh.flatten()

For each (alpha, beta) we check if W_1 = 0 or W_2 = 0

type_of_model = []
for alpha, beta in zip(alphas_mesh, betas_mesh):
    dirty = DirtyModel(alpha=alpha, beta=beta)
    dirty.fit(X, y)
    W1 = abs(dirty.coef_shared_).max()
    W2 = abs(dirty.coef_specific_).max()
    if W1 and not W2:
        type_of_model.append(0)
    elif W2 and not W1:
        type_of_model.append(1)
    elif W1 and W2:
        type_of_model.append(2)
    else:
        type_of_model.append(3)
type_of_model = np.array(type_of_model)

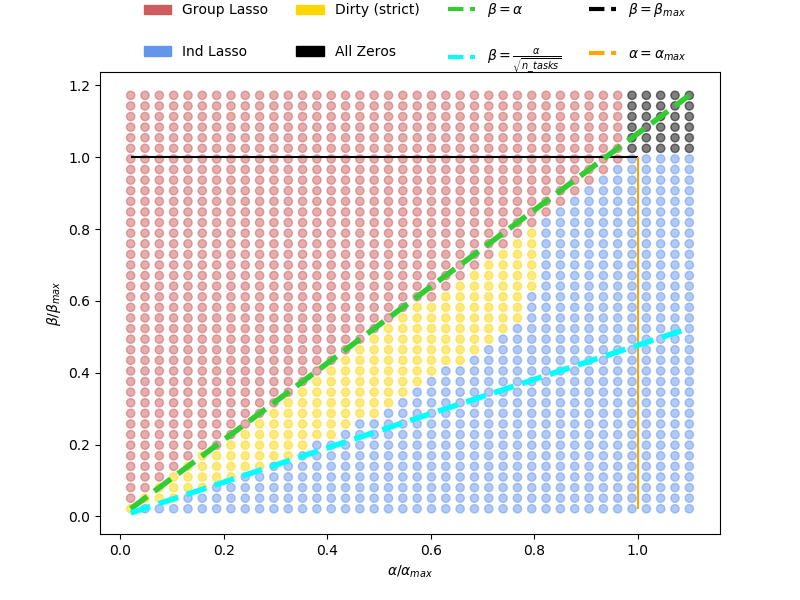
Plot nature of model depending on hyperparameters To benefit from the partial overlap offered by Dirty models, we should pick alpha, beta in the gold area

# We create the legend manually
patch_colors = ["indianred", "cornflowerblue", "gold", "black"]
patch_names = ["Group Lasso", "Ind Lasso", "Dirty (strict)", "All Zeros"]
line_colors = ["limegreen", "cyan", "black", "orange"]
line_names = [r"$\beta = \alpha$",
              r"$\beta = \frac{\alpha}{\sqrt{n\_tasks}}$",
              r"$\beta = \beta_{max}$",
              r"$\alpha = \alpha_{max}$"]
patches = [Patch(color=c, label=name)
           for c, name in zip(patch_colors, patch_names)]
lines = [Line2D([0], [0], color=c, lw=3, ls="--", label=name)
         for c, name in zip(line_colors, line_names)]
legend_handles = patches + lines

# We plot the type of each model
colors = np.array(patch_colors)[type_of_model]
f, ax = plt.subplots(1, 1, figsize=(8, 6))
ax.scatter(alphas_mesh / alpha_max, betas_mesh / beta_max, color=colors,
           alpha=0.5)
ax.plot(alphas / alpha_max, alphas / beta_max, color=line_colors[0], lw=4,
        ls="--")
ax.plot(alphas / alpha_max, alphas / ((n_tasks ** 0.5) * beta_max),
        color=line_colors[1], lw=4, ls="--")
ax.hlines(1., xmin=0.02, xmax=1.0, color="black")
ax.vlines(1., ymin=0.02, ymax=1.0, color="orange")

ax.set_xlabel(r"$\alpha / \alpha_{max}$")
ax.set_ylabel(r"$\beta / \beta_{max}$")
ax.legend(handles=legend_handles, loc=2, ncol=4, bbox_to_anchor=[0.05, 1.18],
          labelspacing=2., fontsize=10, frameon=False)
plt.show()

Estimated memory usage: 10 MB