Comparison of mixed-norm models

This example compares the Group Lasso, Dirty models and multilevel Lasso.

DirtyModel estimates a set of sparse coefficients for multiple regression models that share a fraction of non-zero features. It is a generalization of The GroupLasso estimator. It also takes a 3D X (n_tasks, n_samples, n_features) and a 2D y (n_tasks, n_samples).

DirtyModel solves the optimization problem:

(1 / (2 * n_samples)) * ||Y - X(W_1 + W_2)||^2_Fro + alpha * ||W_1||_21
+ beta * ||W_2||_1

Where:

||W||_21 = \sum_i \sqrt{\sum_j w_ij^2}

i.e. the sum of norm of each row. and:

||W||_1 = \sum_i \sum_j |w_ij|

The multi-level Lasso uses instead a product decomposition. The optimization objective for the Multilevel Lasso is:

    (1 / (2 * n_samples)) * ||Y - XW||^2_Fro + alpha ||W||_{1 0.5}


Where::

    ||W||_{1 0.5} = sum_j sqrt(||W_j||_1)


Which is equivelent to the product decomposition:

    (1 / (2 * n_samples)) * ||Y - X(C[:, None] * S)||^2_Fro
    + beta * ||C||_1 + gamma * ||S||_1

Where::

    C in R^n_features
    S in R^(n_features, n_tasks)
    alpha = 2 * sqrt(beta * gamma)

# Author: Hicham Janati (hicham.janati@inria.fr)
#
# License: BSD (3-clause)

import numpy as np
from matplotlib import pyplot as plt

from mutar import DirtyModel, MultiLevelLasso, IndLasso, GroupLasso

Generate multi-task data

rng = np.random.RandomState(42)
n_tasks, n_samples, n_features = 10, 20, 50
X = rng.randn(n_tasks, n_samples, n_features)

# generate random coefficients and make it sparse
# select support
support = rng.rand(n_features, n_tasks) > 0.97
coef = support * rng.randn(n_features, n_tasks)

# make features 0, 2, 4 and 6 shared
coef[:7:2] = rng.randn(4, n_tasks)

y = np.array([x.dot(c) for x, c in zip(X, coef.T)])

# add noise
y += 0.2 * np.std(y) + rng.randn(n_tasks, n_samples)

Lasso fit

alpha = 0.5 * np.ones(n_tasks)
lasso = IndLasso(alpha=alpha)
lasso.fit(X, y)

Group Lasso fit

alpha = 1.75
gl = GroupLasso(alpha=alpha)
gl.fit(X, y)

Dirty models fit

alpha = 0.8
beta = 0.4
dirty = DirtyModel(alpha=alpha, beta=beta)
dirty.fit(X, y)

Multilevel Lasso fit

alpha = 0.25
mll = MultiLevelLasso(alpha=alpha)
mll.fit(X, y)

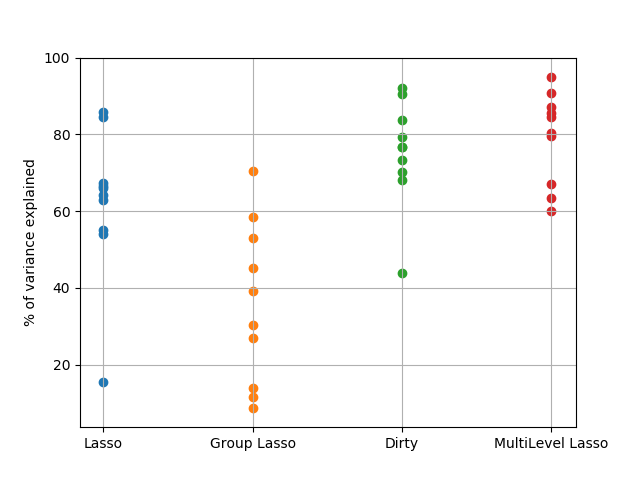
we show the R2 scores for each model. Each dot corresponds to a task.

models = [None, lasso, gl, dirty, mll]
names = ["Truth", "Lasso", "Group Lasso", "Dirty", "MultiLevel Lasso"]

f, ax = plt.subplots(1, 1)
for i, (name, model) in enumerate(zip(names[1:], models[1:])):
    r2 = model.score(X, y)
    ax.scatter(n_tasks * [i + 1], 100 * r2)
ax.set_ylabel("% of variance explained")
ax.set_xticks(np.arange(1, len(models)))
ax.set_xticklabels(names[1:])
ax.grid(True)
plt.show()

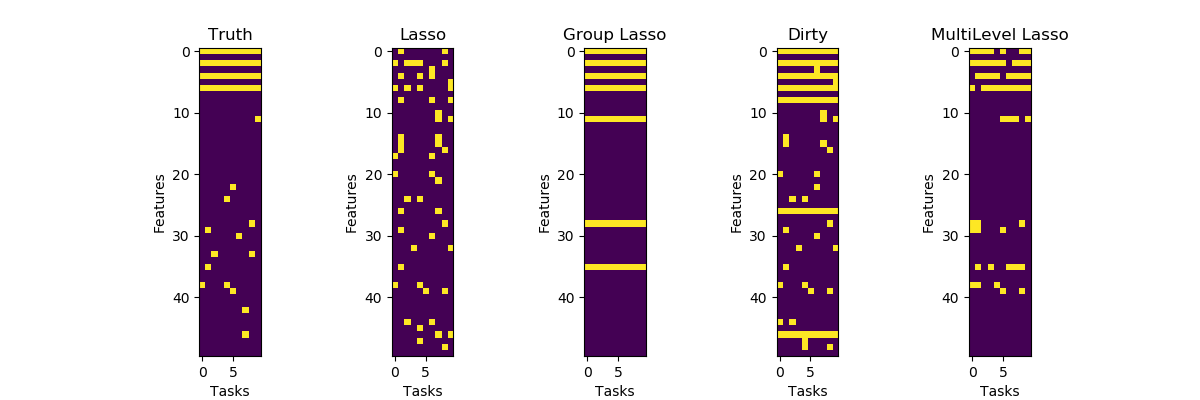
Plot the supports of the true and obtained coefficients for all models

f, axes = plt.subplots(1, 5, figsize=(12, 4))
for i, (ax, model, name) in enumerate(zip(axes, models, names)):
    if i == 0:
        ax.imshow(coef != 0)
    else:
        ax.imshow(model.coef_ != 0)
    ax.set_title(name)
    ax.set_xlabel("Tasks")
    ax.set_ylabel("Features")
plt.show()

Estimated memory usage: 13 MB