Adaptive / Reweighted Lasso

The adaptive or reweighted Lasso minimizes the non-convex L0.5 pseudo norm which is a better sparsity proxy function for the Basis Pursuit L0 norm. In practice, it promotes sparser coefficients with less amplitude bias. As with IndLasso, IndRewLasso is independent across tasks.

IndRewLasso solves the optimization problem:

(1 / (2 * n_samples)) * ||Y - XW||_Fro^2
+ sum_k alpha_k * ||W_k||_0.5

# Author: Hicham Janati (hicham.janati@inria.fr)
#
# License: BSD (3-clause)

import numpy as np
from matplotlib import pyplot as plt

from mutar import IndLasso, IndRewLasso

Generate multi-task data

rng = np.random.RandomState(42)
n_tasks, n_samples, n_features = 2, 20, 100
X = rng.randn(n_tasks, n_samples, n_features)

support = rng.rand(n_features, n_tasks) > 0.95
coef = support * rng.randn(n_features, n_tasks) * 5

y = np.array([x.dot(c) for x, c in zip(X, coef.T)])

# add noise
y += 0.5 * np.std(y) + rng.randn(n_tasks, n_samples)

alpha = 0.05 * np.ones(n_tasks)

Fit the independent Lasso

lasso = IndLasso(alpha=alpha)
lasso.fit(X, y)

Fit the independent reweighted Lasso

rewlasso = IndRewLasso(alpha=alpha)
rewlasso.fit(X, y)

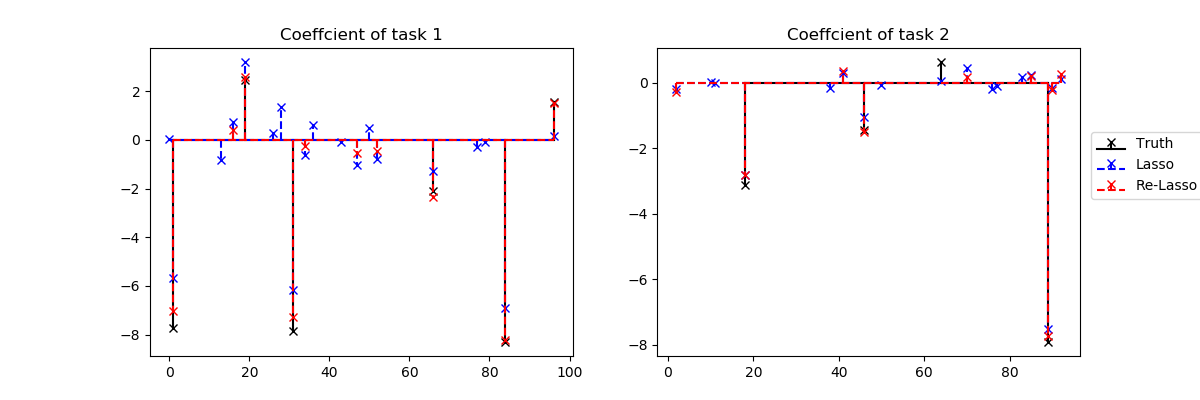
Plot the supports of the true and obtained coefficients. Reweighting reduces the size of the active features and corrects the amplitudes of the relevant coefficients

coefs = [coef, lasso.coef_, rewlasso.coef_]
labels = ["Truth", "Lasso", "Re-Lasso"]
colors = ["k", "b", "r"]
lines = ["-", "--", "--"]
f, axes = plt.subplots(1, 2, figsize=(12, 4))
for c, ll, coefs, label in zip(colors, lines, coefs, labels):
    for i, (ax, coef) in enumerate(zip(axes, coefs.T)):
        # plot non-zero coefs only for clarity
        xx = np.where(coef)[0]
        yy = coef[xx]
        ax.stem(xx, yy, label=label, linefmt=c + ll,
                markerfmt=c + 'x', basefmt=c + ll)
        ax.set_title("Coeffcient of task %d" % (i + 1))
ax.legend(loc=2, bbox_to_anchor=[1.01, 0.75])
plt.show()

Estimated memory usage: 10 MB